TEMAS DE FISICA (APRENDISAJE)

1° TEMA:

TRIÁNGULOS NOTABLES 

algunos triángulos notables son:

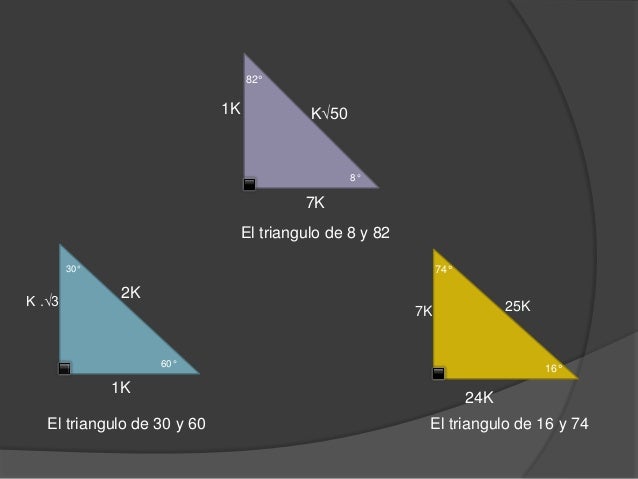
2° TEMA 

DESPEJE DE FORMULAS 

Según el celebre libro "Álgebra Elemental" de Baldor, una fórmula es la expresión de una ley o de un principio general por medio de símbolos o letras. Citando las ventajas del uso de las fórmulas que nos muestra Baldor, tenemos:

1. Expresan de forma breve una ley o un principio general, esto es sin tantas palabras que tengamos que interpretar. Es más fácil decir F=m.a que: la fuerza aplicada es directamente proporcional a la masa de cuerpo multiplicada por la aceleración que este adquiere por motivo de la fuerza aplicada.
2. Son fáciles de recordar. Creo que no es necesario decir ningún ejemplo.
3. Su aplicación es muy fácil, pues para resolver un problema por medio de la fórmula adecuada, basta sustituir las letras por lo valores en el caso dado.

Despeje de variables en una fórmula 

Reglas Para despejar::
1.- Lo que está sumando pasa restando.
2.- Lo que está restando pasa sumando
3.- Lo que está multiplicando pasa dividiendo

4.- Lo que está dividiendo pasa multiplicando
5.- Si está con exponente pasa con raíz.

EJEMPLOS:

En la ecuación x= (at²)/2

a)Despejar “a” 2x/a

Solución:

x = (at²)/2

2x = at²

(2x)/t² = a  --> a = 2x/t²

b) Despejar "t"

Solución

x = (at²)/2

2x = at²

2x/a = t²

√t =  √2x/a  ---> t = √2x/a

3° TEMA

MAGNITUDES

 es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o unarelación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón. Por ejemplo, se considera que el patrón principal de longitud es el metro en el Sistema Internacional de Unidades.

EJEMPLOS:

                                           MEDIR CON UN CENTÍMETRO

4° TEMA:

CLASIFICACIÓN DE MAGNITUDES

Magnitudes Fundamentales:

Son aquellas elegidas arbitrariamente como base para establecer las unidades del Sistema De Unidades y en función de las cuales se expresan las demás magnitudes.
Ejemplo:
Longitud, masa, tiempo, temperatura.

Magnitudes Derivadas: 
Son aquellas magnitudes que se expresan en función de las magnitudes asumidas como fundamentales.
Ejemplo:
Área, volumen, velocidad, aceleración, fuerza, etc. 

Magnitudes Escalares:
Son aquellas que enunciando su valor seguido de su unidad quedan perfectamente definidas, aveces afectado de un signo negativo convencionalmente elegido.Ejemplo: La temperatura -8°CMagnitud Vectorial:
Son aquellas que además de conocer su módulo o valor, es necesario conocer su dirección y sentido para que este claramente definidas.Son magnitudes vectoriales: la fuerza, la aceleración, el desplazamiento, el peso.

5° TEMA:

LA TEORÍA DEL ERROR

definición:     Los conceptos de magnitud física, unidades y medida se han estudiado en la primera lección de Fundamentos Físicos de la Informática y, como complemento, en este capítulo se pretende aprender a estimar los posibles errores en las medidas, así como la propagación de estos errores a través de los cálculos a los resultados, a expresar los resultados y a analizarlos. 

EJEMPLO:

Medir es comparar con un patrón. Por ejemplo, si medimos la anchura del laboratorio poniendo un pie delante de otro, podemos decir que la anchura del laboratorio es 18 pies, siendo nuestro patrón un pie. Ahora bien, una medida nunca puede ser exacta, es decir, siempre cometemos un error, por lo que nuestra medida no será completa sin la estimación del error cometido. Unas veces ese error será debido a los instrumentos de medida, otras a nuestra propia percepción, etc. Los errores al medir son inevitables.En función de la naturaleza del error podemos definir dos tipos de error:

• Errores sistemáticos: Son debidos a problemas en el funcionamiento de los aparatos de medida o al hecho de que al introducir el aparato de medida en el sistema, éste se altera y se modifica, por lo tanto, la magnitud que deseamos medir cambia su valor. Normalmente actúan en el mismo sentido.
• Errores accidentales: Son debidos a causas imponderables que alteran aleatoriamente las medidas. Al producirse aleatoriamente las medidas se distribuyen alrededor del valor real, por lo que un tratamiento estadístico permite estimar su valor.

Debido a la existencia de errores es imposible conocer el valor real de la magnitud a medir. Si somos cuidadosos podemos controlar los errores sistemáticos, en cuanto a los errores accidentales podemos reducirlos si tomamos un conjunto de medidas y calculamos su valor medio. Tomaremos como valor estimado de la medida el valor medio de las distintas medidas realizadas.Supongamos que se pretende medir la longitud L de una barra y se obtienen dos conjuntos de medidas:Grupo a : 146 cm, 146 cm, 146 cm
Grupo b : 140 cm, 152 cm, 146 cmEn ambos casos el valor estimado es el mismo (146 cm). Sin embargo, la precisión de las medidas no es la misma. ¿Cómo podemos diferenciar la precisión de dos medidas? Mediante el concepto de error o incertidumbre que definiremos más adelante.A la hora de expresar una medida siempre se ha de indicar el valor observado junto con su error y la/s unidad/es correspondiente/s. Podemos decir que el valor verdadero de la medida se encuentra con una alta probabilidad en un intervalo cuyos límites son la estimación de la medida más/menos el error estimado.

Medida = Valor observado ± Error       UnidadEn el ejemplo anterior, una vez estimado el error se escribiría: L = 146 ± 4 cm

6° TEMA:

ECUACIONES DIMENSIONALES

es una herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema π de Vaschy-Buckingham (más conocido por teorema π) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:

• Analizar con mayor facilidad el sistema objeto de estudio
• Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.

EJEMPLO:

Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad  dependerá de la altura  y de la gravedad . Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa . Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.

• Identificar las magnitudes de las variables:

• Formar la matriz

• Hacer el producto de matrices:

Aquí tenemos que decir que  se refiere al exponente de la unidad , pero eso se verá en pasos sucesivos.

7° TEMA:

MAGNITUDES VECTORIALES

Magnitudes

Las magnitudes son atributos con los que medimos determinadas propiedades físicas, por ejemplo una temperatura, una longitud, una fuerza, la corriente eléctrica, etc. Encontramos dos tipos de magnitudes, las escalares y las vectoriales. 

Magnitudes vectoriales

En muchos casos las magnitudes escalares no dan información completa sobre una propiedad física. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. Ejemplos de magnitudes vectoriales son la velocidad y la fuerza.



Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.

En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).

8° TEMA :

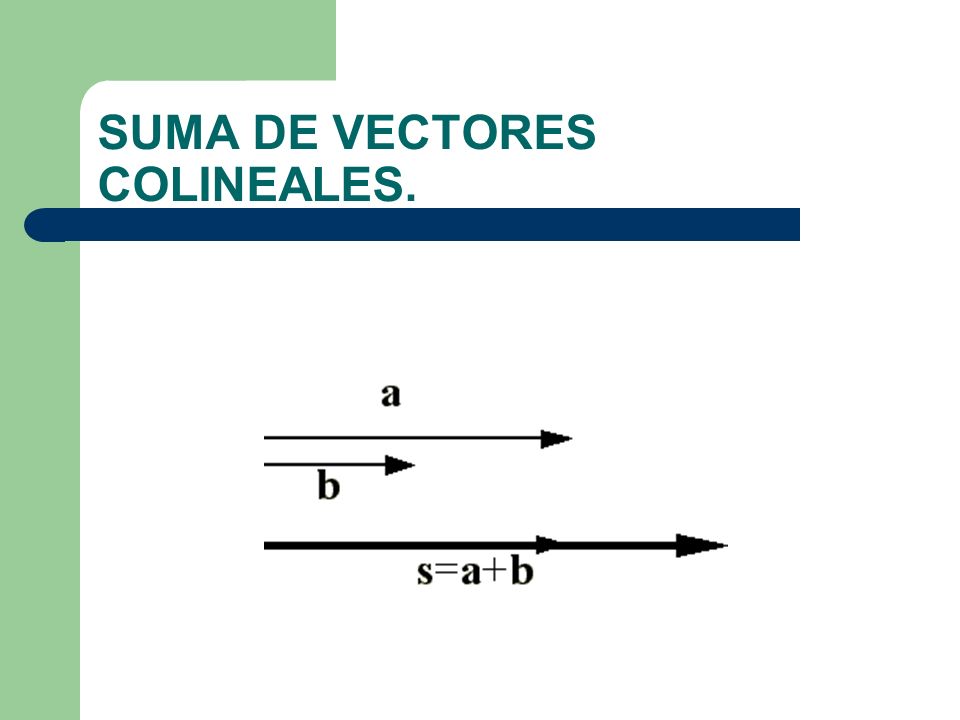
SUMA DE VECTORES COLINEALES

El resultado es igual a la suma algebraica de los módulos de los vectores :

→           → 

x=(x₁, x₂) y= (y₁, y₂)

→ → 

x +y=(x₁+y_1, x₂, y₂)

ejemplos:

9 ° TEMA 

EL MOVIMIENTO

el movimiento es un cambio de la posición de un cuerpo a lo largo del tiempo respecto de un sistema de referencia.

El estudio del movimiento se puede realizar a través de la cinemática o a través de la dinámica. En función de la elección del sistema de referencia quedaran definidas las ecuaciones del movimiento, ecuaciones que determinarán la posición, la velocidad y la aceleración del cuerpo en cada instante de tiempo. Todo movimiento puede representarse y estudiarse mediante gráficas. Las más habituales son las que representan el espacio, la velocidad o la aceleración en función del tiempo.

EJEMPLOS DE MOVIMIENTO:

10° TEMA

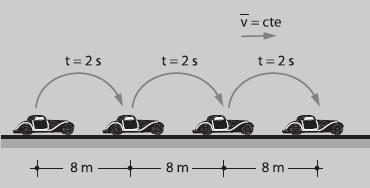
MOVIMIENTO RECTILÍNEO UNIFORME

Un movimiento es rectilíneo cuando un móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Es indicado mediante el acrónimo MRU, aunque en algunos países es MRC, que significa Movimiento Rectilíneo Constante.

• Movimiento que se realiza sobre una línea recta.
• Velocidad constante; implica magnitud y dirección constantes.
• La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
• Aceleración nula.

EJEMPLOS: